加减运算电路实验

加法运算是最基本的算术运算，其运算速度对计算机的运行速度有着重要影响。 4位的加法器可以用4个全加器级联构成，由于存在进位链的传递延时，运算速度随着精度的提高（位数增加）而降低。所以实际的并行加法器并不会采用全加器级联的方法，而是采用先行进位加法器。

由于补码加法可以连同符号位在内一起运算，并且补码减法可以转换为加法，所以在计算机中通常采用补码进行加减运算。其基本公式如下：

这两个公式是补码加减运算的理论依据，它们所包含的意义是：

也就是说可以利用二进制加法器进行补码加减运算，只需要在加法器的基础上增加求补电路就可以实现减法，无需为减法设计专门的电路。 根据上述原理可以设计出补码加减运算电路如图 1所示。

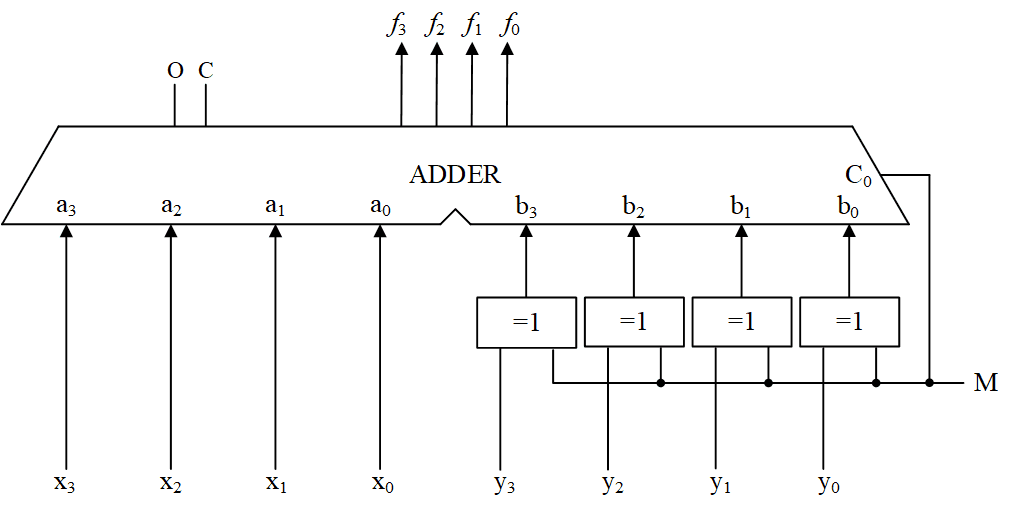
图中ADDER是二进制加法器，实现的加法运算为F＝A+B+C0；其中a_i=x_i，b_i=y_i⊕M，C0=M。

当M=0时，b_i=y_i⊕0=y_i，C0=0，所以F=X+Y； 当M=1时，， C0＝1，故 。

可见，M用来控制是将Y送到加法器运算，还是将Y求相反数后再相加。 当M=0时做加法运算，M=1时做减法运算。

溢出（overflow）是指运算结果超出了数的表示范围。 通过上面的讨论可知，有符号数的补码加减运算和无符号数的加法运算可以用同一个电路实现。 对于4位二进制编码，无符号数的表示范围是0～15，补码表示的带符号数的范围是−8～+7。 如果用图 1电路进行无符号数运算，结果大于15会产生进位，因此根据进位C值就可以判断无符号数的加法是否溢出。 但是补码加法运算是否溢出并不能根据进位来判断。下面介绍一种便于实验电路实现的补码加法运算的溢出检测方法——根据两个操作数的符号位和结果的符号位是否一致进行判断。

两个参加运算的数据如果符号相异，做加法时是不会产生溢出的。只有两个相同符号的数做加法运算时才有可能产生溢出。换句话说，两个正数相加结果为负数，或者两个负数相加结果为正数，均表示运算结果溢出。检测方法如下：

假设As和Bs表示两个操作数的符号，Fs表示运算结果的符号，则溢出检测的逻辑表达式为：

当两个加数为负数（As=Bs=1），而结果为正数（Fs=0）时，或者当两个加数为正数（As=Bs=0），而结果为负数（Fs=1）时，OV＝1，即发生溢出。

理解实验原理，按照图 1设计加减运算电路。 参考电路如图 2所示。

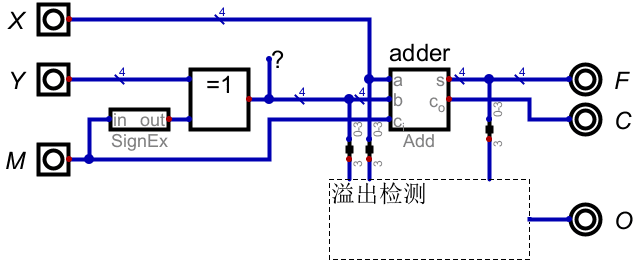
下面给出几点说明。