算术逻辑单元实验
实验原理
计算机除了能够进行加减运算,还要能够进行逻辑运算。实现加减运算和逻辑运算的电路称为算术逻辑单元(ALU,Arithmetic Logic Unit)。图 1是一个简单ALU的设计,虚线框内是前面实验完成的加减运算电路,只是简化了画法,将4位数据用一根较粗的信号线表示;增加了与(AND)、或(OR)、异或(XOR)逻辑运算,并通过一个四选一多路器选择运算的功能。
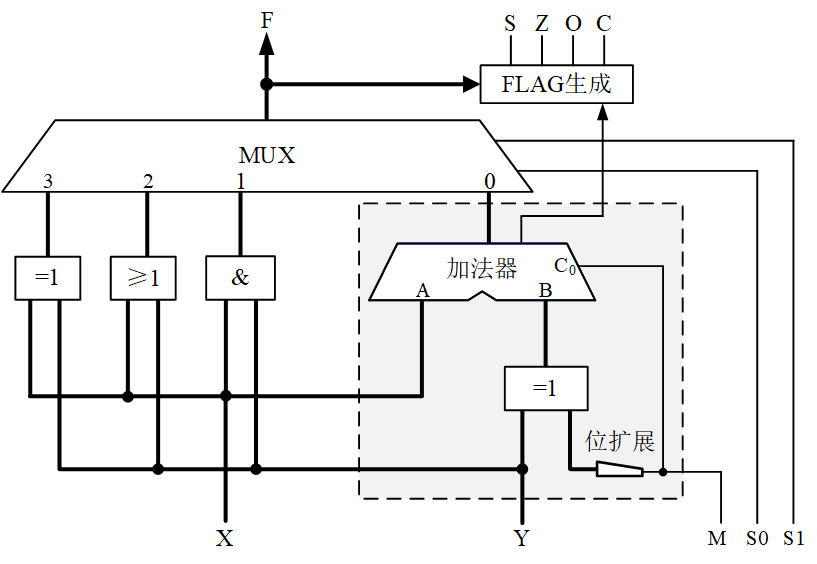
该ALU电路没有用非门实现逻辑非(NOT)运算,这是因为异或1可以实现取反。通过使Y各位全为1,选择异或运算可以实现对X的非运算。
图 1电路还产生S、Z、O、C四个运算结果的特征标志,通常用于数值大小的比较判断,在后面的实验中将会用到。这四个标志的含义如下。
-
SF(Sign Flag):符号标志。
SF=1表示结果为负数,SF=0表示结果为正数。
-
ZF(Zero Flag):零标志。
ZF=1表示结果为零,ZF=0表示结果非零。
-
OF(Overflow Flag):溢出标志。
OF=1表示结果溢出,OF=0表示结果不溢出;。
-
CF(Carry Flag):进位标志。
CF=1表示有进位,CF=0表示没有进位。
OF和CF由加法器产生,在前面的实验中已经完成。这个实验还需要完成符号标志和零标志的检测电路。 因为运算结果的最高位就是符号位,所以符号标志的生成逻辑非常简单,逻辑方程如下:
SF=FS
一种简单的零标志生成方法是,将运算结果的每一位进行或运算,如果结果为0,则零标志为1。以4位二进制为例,产生零标志的逻辑方程如下:
| 进位标志和溢出标志必须由加法电路产生,而零标志和符号标志通常根据ALU的运算结果产生。如果逻辑运算的结果为零,零标志也会为1。 |
预习要求
-
理解实验原理。
-
阅读第一章Digital仿真软件使用指南的“层次化设计”。
实验任务
1.设计任务
理解实验原理,按照图 1设计电路。其中加减运算电路使用前面实验完成的,将其作为子电路。 有关添加子电路的方法,请参考第一章Digital仿真软件使用指南的“层次化设计”。 MUX多路器组件曾在多路选择器实验中使用过,这里要将选择位的位数设置为2,以构成4选1多路器。
|
2.测试任务
-
编写测试数据。
例 1. ALU测试数据举例X Y M S1 S0 F S Z O C 0b0011 0b0101 0 0 0 0b1000 1 0 1 0
-
执行测试。
保存测试结果数据用于实验报告的实验结果分析。
测试的目的是检查逻辑设计错误而非连接错误。若要检查电路连接是否有误,可在执行测试前先启动仿真;若启动仿真出错,可根据报错信息改正连接错误。 -
实验结果分析
对测试结果数据进行分析并给出结论。
算术运算可参考加减运算电路实验的验证任务要求和记录表样式。